3 31 honeycomb

331 honeycomb
(no image)
Type Uniform tessellation
Schläfli symbol {3,3,3,33,1}
Coxeter symbol 331
Coxeter–Dynkin diagram
7-face types 321
{36}
6-face types 221
{35}
5-face types 211
{34}
4-face type {33}
Cell type {32}
Face type {3}
Face figure 031
Edge figure 131
Vertex figure 231
Coxeter group 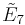{\tilde{E}}_7, [33,3,1]
Properties vertex-transitive

In 7-dimensional geometry, the 331 honeycomb is a uniform honeycomb, also given by Schlafli symbol {3,3,3,33,1} and is composed of 321 and 7-simplex facets, with 56 and 576 of them respectively around each vertex.

Its vertex arrangement is called the E7 lattice.[1]

Contents

Construction

It is created by a Wythoff construction upon a set of 8 hyperplane mirrors in 7-dimensional space.

The facet information can be extracted from its Coxeter–Dynkin diagram.

Removing the node on the short branch leaves the 6-simplex facet:

Removing the node on the end of the 3-length branch leaves the 321 facet:

The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes 231 polytope.

The edge figure is determined by removing the ringed node and ringing the neighboring node. This makes 6-demicube (131).

The face figure is determined by removing the ringed node and ringing the neighboring node. This makes rectified 5-simplex (031).

The cell figure is determined by removing the ringed node of the face figure and ringing the neighboring nodes. This makes tetrahedral prism {}×{3,3}.

Kissing number

Each vertex of this polytope is the center of a 6-sphere in the densest known packing in 7 dimensions; its kissing number is 126.

See also

References

  1. ^ http://www2.research.att.com/~njas/lattices/E7.html